fractale

Se dit d'objets mathématiques dont la création ou la forme ne trouve ses règles que dans l'irrégularité ou la fragmentation ; se dit des branches des mathématiques qui étudient de tels objets.

Les mathématiciens ont, de tout temps, cherché à étudier les formes simples (nombres entiers, droites, cercles, etc.) ou à simplifier les formes complexes. Avec les fractales, c'est plutôt le chemin inverse qui a été suivi.

Partant de processus répétitifs très simples, les mathématiciens ont fait apparaître le désordre, mais un désordre particulier, prévisible, qui peut se lire et se mesurer simplement, à l'aide d'algorithmes élaborés et traités par ordinateur.

Historique

Des monstres mathématiques

De nombreuses notions mathématiques ont d'abord été regardées comme des « monstres » dont on ne parlait qu'à mots couverts avant de les domestiquer, pour les trouver alors extrêmement fertiles. Il en a été ainsi chez les pythagoriciens avec l'apparition des nombres irrationnels, à la Renaissance avec celle des nombres négatifs et des nombres complexes.

Le xix^e s. est particulièrement riche en monstres mathématiques. C'est en effet la période où une exigence de rigueur de plus en plus poussée remet en cause beaucoup d'énoncés admis jusque-là sans démonstration. Georg Cantor, notamment, multiplie les monstres, qu'il étudie avec parfois beaucoup d'incrédulité (« Je le vois mais ne le crois pas », écrit-il à Richard Dedekind).

Ces travaux remettent en question la notion de fonction et débouchent sur un édifice entièrement repensé, en liaison avec la théorie des ensembles et la topologie.

L'homothétie interne des fractales : l'apport de Mandelbrot

À partir de 1960, Benoît Mandelbrot, mathématicien français expatrié aux États-Unis, développe grâce aux ordinateurs une étude plus systématique de ces formes complexes, qu'il désigne d'un nouveau nom : les « fractales ». Ce mot, qui se rapproche de « fractionné », « fragmenté », « fracturé », est à relier à une notion élémentaire et importante : l'homothétie interne, qui fournit un outil simple pour construire ces objets, étudier leur degré de complexité et déboucher sur la notion de dimension non entière, ou fractale.

La théorie des fractales de Mandelbrot voit le jour en 1975 avec la publication de son essai intitulé les Objets fractals : forme, hasard et dimension. S'il existait déjà depuis plus d'un siècle des objets fractals, sans toutefois qu'ils portent ce nom, ils n'avaient été créés qu'en tant qu'anomalies ou contre-exemples afin de prouver la non-équivalence de certaines notions : continuité et dérivabilité des fonctions (fonction de Weierstrass, premier exemple de fonctions partout continues et nulle part dérivables, et donc impossibles à dessiner) ou cardinal et mesure d'un ensemble (ensemble de Cantor, courbe de Peano ou de Sierpiński).

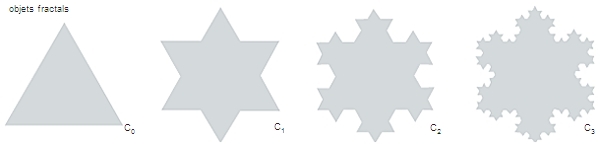
La courbe de Helge von Koch, dite « flocon de neige », qui date de 1904, résume parfaitement l'idée des fractales. C'est la courbe limite de la suite polygonale (C_n) construite par récurrence : partant d'un triangle équilatéral, on ajoute un nouveau triangle équilatéral au tiers central de chacun des segments composant la courbe précédente. Ainsi, au fur et à mesure que l'on répète l'opération, le « flocon » voit ses côtés se hérisser de pointes de forme équilatérale de plus en plus petites. Cette courbe n'est ni différentiable ni rectifiable ; sa mesure est infinie : elle est la limite de celles des courbes 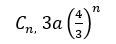[a étant la mesure du côté du triangle initial], et pourtant son aire est finie et égale à 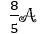( 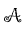étant l'aire de l'intérieur de C₀). Elle semble figurer, au moins partiellement, une côte rocheuse très découpée. Un autre problème serait alors de calculer la longueur de cette côte.

Exemples et applications

La nature fournit de nombreux autres exemples de systèmes présentant un caractère fractal : ramification des bronches et bronchioles, ramification d'un réseau hydrographique, forme des chaînes montagneuses, mouvement brownien, etc. Les fractales trouvent aujourd'hui de très nombreuses applications dans les sciences : elles apparaissent notamment en physique, dans la théorie du chaos et dans la mécanique des turbulences ; en astronomie, dans la répartition des galaxies ; en biologie, dans la structure des plantes et de certains êtres vivants… Enfin, elles fournissent aux graphistes une source d'inspiration esthétique et une méthode pour simuler la végétation ou le relief géographique.

Quelle est la longueur de la côte de la Bretagne ?

À la question ci-dessus, il n'y a pas une bonne réponse mais plusieurs : tout dépend de l'échelle. Mandelbrot arrive à cette conclusion a priori étonnante par le processus suivant : à partir d'une série de photographies prises à 10 000 m d'altitude, on calcule, grâce au coefficient d'homothétie, la longueur de la côte visible avec un pouvoir de séparation de l'ordre du décamètre ; si l'on répète la même opération par le même procédé à 500 m d'altitude, les photographies font apparaître des détails au mètre près, la côte est plus précise, et sa longueur… plus grande. Si les mesures se font ensuite au sol, la longueur de la côte augmente encore. En allant encore plus loin dans la précision, galet par galet, molécule par molécule, atome par atome, on arriverait vite à une longueur infinie. Plus l'instrument de mesure s'affine, plus la longueur augmente, car une fraction de la côte au niveau du sol reste aussi complexe que la côte entière vue à 10 000 m d'altitude.

Le bestiaire des courbes fractales

L'aspect fantastique de ces créations mathématiques aux allures étranges est indéniable.

En 1904, Helge von Koch avait trouvé une courbe continue et non dérivable qui, déjà, était plus visuelle que les monstres découverts par Cantor. On définit cette courbe, dite flocon ou île de von Koch, par récurrence : partant d'un triangle équilatéral, on ajoute un nouveau triangle équilatéral au tiers central de chacun des segments composant la courbe précédente. La limite de la courbe obtenue est étonnante : enfermée dans un espace limité, cette courbe a une longueur infinie.

D'autres fractales peuvent être aisément construites par pliages. Michel Mendès France a démontré que tout nombre réel transcendant (qui n'est pas solution d'une équation polynomiale à coefficients entiers ou rationnels, comme π, e, mais aussi beaucoup d'autres nombres) peut être représenté par une courbe fractale et, inversement, que toute courbe obtenue comme limite d'un tel pliage automatique peut représenter un tel nombre. L'ensemble des nombres transcendants est obtenu en rompant à chaque fois la répétition, le sens de pliage (en brisant la symétrie).

Des dimensions fractionnaires

Pour des objets de dimensions finies dans une enveloppe infinie, on peut calculer facilement la longueur, l'aire ou le volume, mais aussi les classer suivant leur degré de complexité, appelé dimension fractale par Mandelbrot.

Le flocon de von Koch fait apparaître un coefficient de 4/3 : à chaque étape, la longueur, multipliée par 4/3, tend vers l'infini, sa surface augmente de triangles qui mesurent le quart de l'aire des triangles ajoutés à l'étape précédente. L'aire totale du flocon a pour limite 2√3/5, en partant d'un flocon de surface unitaire.

Plus généralement, remplacer un segment par n segments plus petits dans un rapport k fera apparaître un coefficient d'homothétie égal à n/k.

La dimension d'homothétie

Mandelbrot a défini une notion de dimension qui permet de classer les objets fractals tout en restant en accord avec la dimension topologique classique de ces objets plus simples :
– un segment de dimension topologique 1 est la réunion de trois segments de longueur 1/3, ou de quatre de longueur 1/4 ;
– un carré de dimension topologique 2 est la réunion de neuf carrés de longueur 1/3 ou de seize carrés de longueur 1/4 ;
– un cube de dimension topologique 3 est la réunion de vingt-sept cubes de longueur 1/3 ou de soixante-quatre cubes de longueur 1/4.

Dans chaque cas, la dimension – notée d – est liée au nombre d'éléments constituants – noté n – et au rapport d'homothétie 1/k par la relation : n = (1/k)^d. Cela permet d'exprimer d en fonction de n et de k grâce aux logarithmes : d = –log n/log k.

Étendue aux objets fractals, cette relation donne des dimensions fractionnaires ou fractales : log 4/log 3 ≈ 1,26 pour le flocon de von Koch, log 2/log 3 ≈ 0,63 pour la construction triadique de Cantor, log 9/log 3 = 2 pour la courbe de Peano (qui recouvre le carré)…

Formes et dimensions de la nature

Mandelbrot a donné de nombreux exemples où les notions d'homothétie interne et de dimension fractale apparaissent dans les formes complexes de la nature.

La longueur d'une côte, le relief d'une montagne jeune ou d'une île montagneuse, un réseau fluvial, la forme des arbres, le réseau des veines et des artères, les lignes de fracture en métallurgie, la forme des nuages et leur répartition dans le ciel, celle des étoiles dans une galaxie, la surface des substances favorisant la catalyse, la répartition des mots dans un texte sont autant d'exemples d'objets fractals que l'on peut décrire quantitativement.

Comme l'a fait remarquer Mandelbrot, la géométrie naturelle est le plus souvent une géométrie des formes complexes, qu'il appelle géométrie fractale, tandis que la géométrie de la droite, du cercle, des objets réguliers est le plus souvent celle de la création humaine.

Fractales et astrophysique

Selon de nombreux astrophysiciens, la répartition des galaxies dans l'espace pourrait être fractale. La théorie de la formation des étoiles et des galaxies de Fred Hoyle, le modèle descriptif d'Edmund Edward Fournier d'Albe et un grand nombre de données empiriques suggèrent une large zone de similitude interne dans laquelle la dimension fractale serait voisine de 1.

Fractales et matériaux

La structure de nombreux matériaux, naturels ou synthétisés, relève aussi de la géométrie fractale. Tel le cas de matériaux polymères, de certaines surfaces rugueuses ou de corps poreux. Diverses mesures suggèrent également que les surfaces de fracture dans les métaux peuvent avoir un caractère fractal.

La structure fractale de certains matériaux nouveaux leur confère des propriétés exceptionnelles. Les chimistes ont pu récemment synthétiser des matériaux de structure extrêmement ténue, tels que des gels de silice, dont la densité est de l'ordre de 50 kg/m³. Cette densité est intermédiaire entre celle d'un gaz (de l'ordre de 1 kg/m³) et celle d'un liquide ou d'un solide (de l'ordre de 1 000 kg/m³). De tels matériaux, ultralégers, sont appelés aérogels. Leurs propriétés surprenantes (faible densité, très grand pouvoir d'isolation thermique) sont liées à leur structure fractale.

Fractales et images de synthèse

Un facteur prépondérant qui a permis l'extension très rapide de l'étude des fractales et son application à un nombre croissant de disciplines est le formidable développement de l'outil informatique. Celui-ci permet non seulement des calculs toujours plus complexes, mais surtout la réalisation d'images de qualité toujours plus remarquable. Certaines de ces images se révèlent être d'une étonnante beauté. La coexistence de traits de tailles très diverses, l'existence d'un ordre hiérarchique qui structure des milieux en apparence complètement désordonnés ont permis à nombre d'artistes d'élaborer des figures d'une grande richesse et d'une grande diversité. À ce titre, il faut citer les simulations d'objets naturels, tels les paysages imaginaires de Richard Voss, ou des images purement abstraites, infiniment complexes malgré la simplicité de leur règle de construction.

Des reliefs fractals

C'est encore Mandelbrot qui, le premier, a eu l'idée d'introduire l'aléatoire dans ses algorithmes. À partir d'une courbe très simple, d'une ligne ou d'un triangle, on choisit au hasard, à chaque étape et pour chaque segment ou triangle, entre deux transformations polygonales. Et l'on répète l'opération à des échelles de plus en plus petites. Le réalisme de l'image dépend du choix du générateur de nombres aléatoires.

Les ensembles de Julia

Un autre procédé pour obtenir des objets fractals fut redécouvert dans les années 80 par Mandelbrot à partir des travaux de Gaston Julia et Pierre Fatou, et généralisé grâce aux ordinateurs. Ce procédé consiste à étudier le comportement de la famille de fonctions qui à un nombre complexe associe son carré augmenté d'une constante, elle aussi complexe, lorsque l'on réitère le calcul à partir des résultats précédents.

Cela revient à choisir un nombre Z_o de départ et une constante C, et à faire tourner indéfiniment la machine à partir de l'algorithme suivant :
 Z_n → Z_n² → Z_n + 1 = Z_n² + C, puis à observer ce qui se passe.

Dans le cas le plus simple, où Z₀ est un nombre réel positif et où la constante C est égale à 0, l'itération de la fonction conduit à 0 si Z₀ est inférieur à 1, donne constamment 1 pour Z₀ égal à 1 et diverge vers l'infini pour Z₀ supérieur à 1. On peut dire que Z₀ = 1 est une frontière entre deux bassins d'attraction avec 0 et l'infini comme attracteurs.

Mandelbrot découvrit que lorsque la constante C n'est pas nulle, non seulement il peut exister plusieurs points attracteurs, mais, de plus, les frontières séparant les bassins d'attraction deviennent extrêmement compliquées et étranges. Mandelbrot appela ces courbes frontières les ensembles de Julia.

Des fractales au chaos

Un comportement indécidable apparaît en météorologie dans les prévisions à plus de quinze jours, en biologie dans la croissance de populations d'animaux ou de virus, en électronique dans la propagation des bruits, ou en mécanique dans la trajectoire d'objets célestes comme les planètes de notre système solaire.

De l'ordre au désordre

Mettez deux boules en présence : une très grosse qui sert de repère et une petite qui tourne autour de la première. Depuis Newton, astronomes et mathématiciens savent parfaitement décrire ce qui va se passer au fil du temps : selon sa position et sa vitesse à un instant donné, la petite boule va être attirée par la grosse et s'en approcher en décrivant une trajectoire elliptique ou, au contraire, s'en éloigner définitivement. L'avenir de ce système est entièrement déterminé par les conditions initiales mesurées à un instant donné.

Régi par ces lois, le système solaire, malgré sa complexité, paraît être un gigantesque mouvement d'horlogerie. Représenté par un ensemble d'équations linéaires et obéissant aux règles de la mécanique laplacienne, il constitue un système entièrement déterministe.

Introduisez un troisième corps dans ce système fermé et tout change. Dans le champ gravitationnel créé par ces trois corps, le désordre apparaît ; c'est le chaos, autrement dit l'impossibilité de prévoir ce qu'il adviendra de chacun de ces objets au cours du temps, surtout s'il est très long, bien que toutes les conditions initiales soient connues et que le système puisse être mis en équations (différentielles).

Le système est déterministe mais… imprévisible. À deux états très voisins à un instant donné peuvent correspondre, à plus ou moins long terme, des comportements totalement différents, le système étant trop sensible aux conditions initiales. Ces phénomènes, déjà entrevus par Jacques Hadamard et Henri Poincaré au début du xx^e s., ont été mis en évidence depuis 1960, grâce aux ordinateurs, par de nombreux scientifiques : c'est le domaine des « systèmes dynamiques ».

Des fractales aux attracteurs étranges

Comment ces phénomènes dynamiques sont-ils décrits géométriquement ? Les topologistes les représentent par une trajectoire, un écoulement dans un espace dont la dimension dépend du nombre de paramètres choisis. À chaque instant, l'état du système est représenté par un point dans cet espace, appelé espace des phases. L'évolution du système est décrite par la trajectoire de ce point. Pour les phénomènes les plus simples, ce point est attiré vers un point d'équilibre ou une courbe limite près de laquelle il repasse périodiquement. Les mathématiciens appellent ces courbes limites des attracteurs.

Pour les systèmes chaotiques, les attracteurs sont des courbes plus complexes qui, pour les phénomènes dissipatifs, présentent une symétrie d'homothétie interne : si l'on fait un grossissement en certaines parties de l'attracteur, on y retrouve la même forme, la même structure à une autre échelle. Ces courbes sont des fractales. Le désordre est dans le système, mais l'ordre apparaît dans ses représentations géométriques. Le chaos déterministe est caractérisé par ce type d'attracteurs, que les mathématiciens appellent attracteurs étranges.